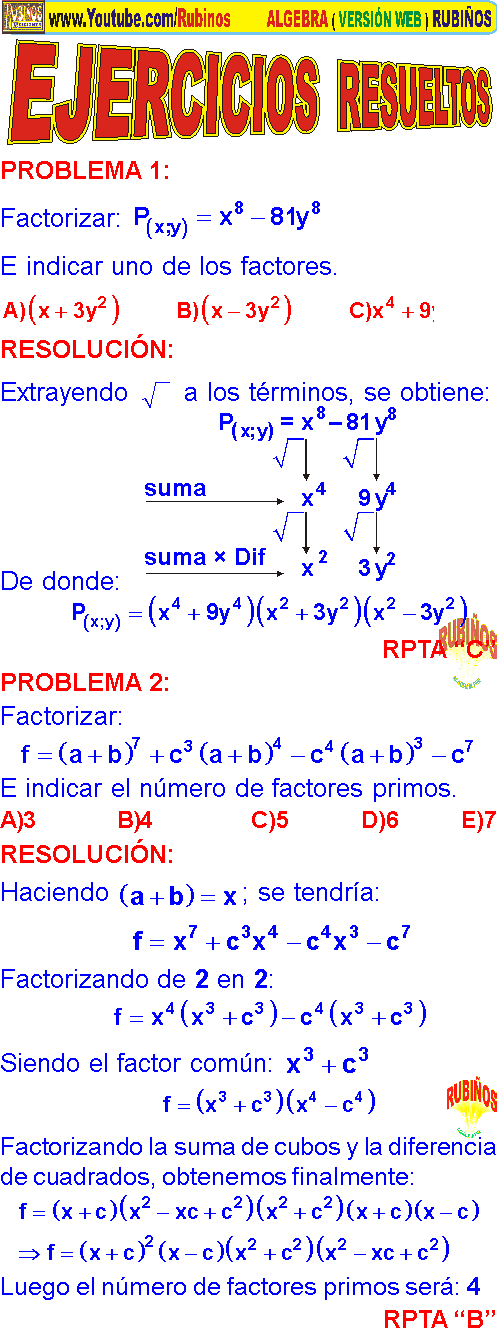
FACTORIZACIÓN DE POLINOMIOS PROBLEMAS RESUELTOS
Al factorizar un polinomio lo descomponemos como una multiplicación y contribuye cuando queremos resolver ecuaciones o inecuaciones polinomiales.
Por ejemplo, para resolver una ecuación cuadrática debemos factorizar el polinomio cuadrático con el método del aspa simple.
- CLIC AQUÍ Ver TEORÍA DE FACTORIZACIÓN PDF
- Ver EJERCICIOS RESUELTOS
- Ver FULL PROBLEMAS RESUELTOS
- Ver PRACTICA CON RESPUESTAS
- Ver VIDEOS
Factorice el polinomio
M(m; n) =m³n – n³m
A) mn(m+n+ 1)
B) m(m+n)(m – n)
C) mn(m+n)(m – n)
D) (m+n)(m – n)
Rpta. : "C"
PROBLEMA 2 :
Indique la suma de factores primos de
f(a; b) =a² – 2a+1 – b²
A) 2b+2
B) 2a+a
C) 2a – 2
D) a – 2
Rpta. : "C"
PROBLEMA 3 :
Determine el número de factores primos de la siguiente expresión polinomial.
P(a; b) = (a+b)³(a – b) – (a – b)³(a+b)
A) 2
B) 1
C) 4
D) 3
Rpta. : "C"