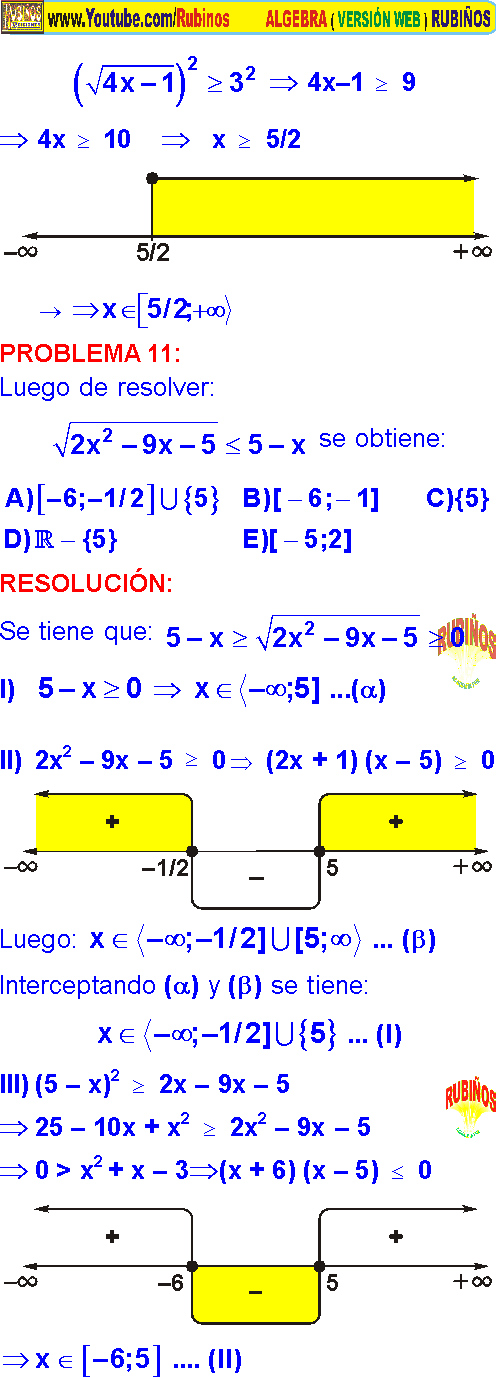
INECUACIONES DE GRADO SUPERIOR E IRRACIONALES PROBLEMAS RESUELTOS
Ahora se amplia el estudio de las inecuaciones analizando polinomios de grado mayor a 2 y el estudio de las inecuaciones fraccionarias.
Este tema tendrá un importante papel al momento de calcular el dominio y rango de una función.
Se utiliza para modelos de optimización.
EJERCICIO 1 :
Un niño preguntó a su abuelo por su edad, a lo que éste respondió: ”Si a mi edad agregas cinco años menos que la mitad de lo que tengo, tendría más de 76 años”. ¿ Qué edad, como mínimo, tiene el abuelo?
A) 54
B) 53
C) 55
D) 56
E) 57
Rpta. : "C"
EJERCICIO 2 :
Se quejaba un burro de su pesada carga a lo que otro le respondió: “ Entre los dos llevamos juntos 27 Kilos, pero lo que a mí me ha tocado es poco menos que el doble de lo que tú llevas”. El primero replicó: “Sí, pero a pesar de mi edad; lo que tu llevas excede en más de 5 kilos a lo que yo llevo”.
¿Cuánto llevaba el que cargaba más, si ambos portaban una cantidad entera de kilos?
A) 17K
B) 19K
C) 18K
D) 16K
E) 20K
Rpta. : "A"
EJERCICIO 3 :
Entre Pa y Pedro tienen juntos 32 años. Pa es mayor que Pedro, pero si aquel tuviera 7 años menos y éste último 8 años más, el primero tendría menos años que la mitad de la del segundo.
¿Qué edad tiene Pa?
A) 12
B) 17
C) 19
D) 14
E) 16
Rpta. : "B"