RELACIÓN MATEMÁTICA EJERCICIOS RESUELTOS NIVEL BÁSICO
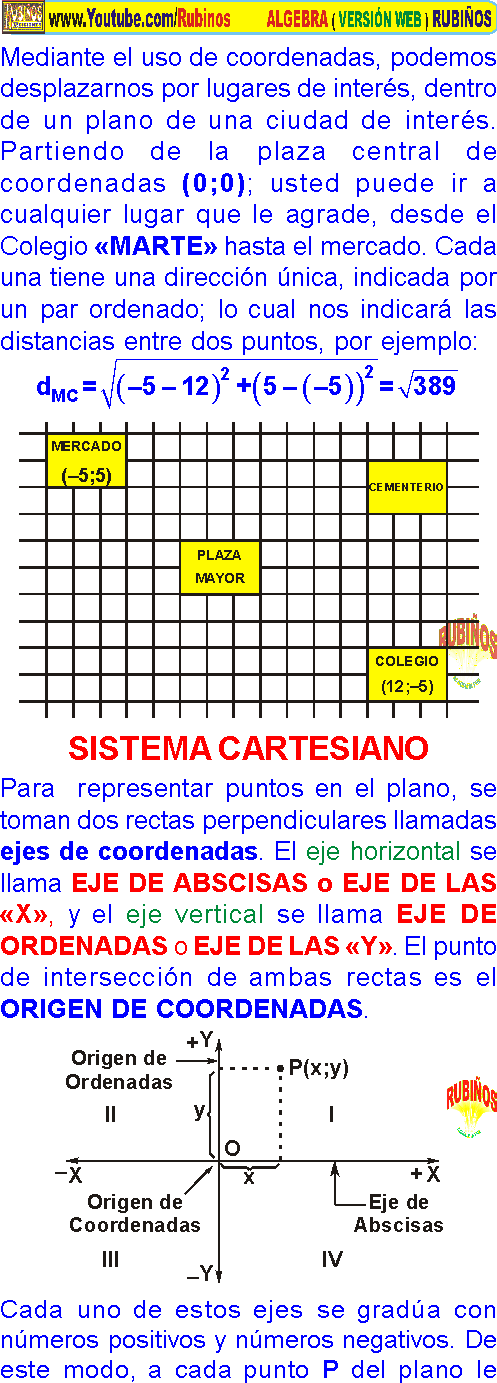
Mediante el uso de coordenadas, podemos desplazarnos por lugares de interés, dentro de un plano de una ciudad de interés. Partiendo de la plaza central de coordenadas (0;0); usted puede ir a cualquier lugar que le agrade, desde el Colegio «MARTE» hasta el mercado. Cada una tiene una dirección única, indicada por un par ordenado; lo cual nos indicará las distancias entre dos puntos, por ejemplo: SISTEMA CARTESIANO Para representar puntos en el plano, se toman dos rectas perpendiculares llamadas ejes de coordenadas. El eje horizontal se llama EJE DE ABSCISAS o EJE DE LAS «X», y el eje vertical se llama EJE DE ORDENADAS o EJE DE LAS «Y». El punto de intersección de ambas rectas es el ORIGEN DE COORDENADAS. Cada uno de estos ejes se gradúa con números positivos y números negativos. De este modo, a cada punto P del plano le corresponde un par de números (x,y) que llamamos coordenadas del punto. Las coordenadas de un punto P(x,y) están dadas por un par ordenado de números, el primero «x», denominado abscisa, y el segundo «y» denominado ordenada. La primera coordenada «x» corresponde al eje horizontal y el segundo «y» al eje vertical. Ejemplo: Aquí tenemos una cuadrícula con dos ejes numerados, uno vertical y otro horizontal, que se cortan en el punto O. Sobre la cuadrícula esta dibujado el mapa del Perú haciendo coincidir el punto O en Lima. Del gráfico se observa: PAR ORDENADO : Es un conjunto de dos elementos con la propiedad de que a uno de ellos se le considera el primer elemento y al otro el segundo elemento. Si dichos elementos son a y b, el par ordenado se representa por: IGUALDAD DE PARES ORDENADOS : Para que dos pares ordenados sean iguales sus «primeras» y «segundas» componentes deben ser iguales. Es decir: Ejemplo 1 : Si son pares ordenados iguales porque: 27 = 40 – 13 ; 3 = 1 + 2 Ejemplo 2 : Si . Hallar: «x+y» Si son pares ordenados iguales, se debe cumplir que: x + 8 = 15 y Þ x = 7 Þ y = 4 Luego: x + y = 7 + 4 = 11 PRODUCTO CARTESIANO Dados dos conjuntos A y B no vacíos, se llama producto cartesiano de A por B, al conjunto formado por todos los pares ordenados (a; b) tales que . Ejemplo: Sea: A = {1;2} ; B = {5;7} Hallar: a) A × B y b) B × A Resolución: A × B = {(1;5), (1;7), (2;5), (2;7)} B × A = {(5;1), (5;2), (7;1), (7;2)} OBSERVACIÓN : Como te podrás dar cuenta: A × B B × A, es decir el producto cartesiano no es conmutativo. REPRESENTACIÓN GRÁFICA DEL PRODUCTO CARTESIANO Dados: E = {a ; b ; c} y F = {1 ; 3} E×F={(a;1),(a;3),(b;1),(b;3),(c;1),(c;3)} Este producto puede ser representado gráficamente de las siguientes maneras: i) matricial : Es un cuadrado de doble entrada, en donde los elementos del primer conjunto se escriben en la primera columna, y los del segundo conjunto en la primera fila. En los cuadrados internos se encuentran los elementos del producto cartesiano. ii) sagital : Esta representación es mediante un diagrama de Venn se le denomina sagital porque se emplean flechas para relacionar los elementos. iii) cartesiana : Se realiza en el sistema cartesiano, en el eje horizontal se ubican los elementos del primer conjunto y en el eje vertical del segundo conjunto. iv) diagrama del arbol : relación binaria : Dados dos conjuntos A y B, se dice que R es una relación de A en B, si es subconjunto del producto cartesiano A × B. Simbólicamente, se denota así: R: Donde: R: A B, se lee: «R es una relación de A en B» Ejemplo: Sea: A = {5; 8; 11} y B = {4; 7; 10} Hallar: R = {(a,b) A×B / a