FUNCIONES EXPONENCIALES Y LOGARITMICAS FORMULAS - EJEMPLOS Y GRAFICAS PDF
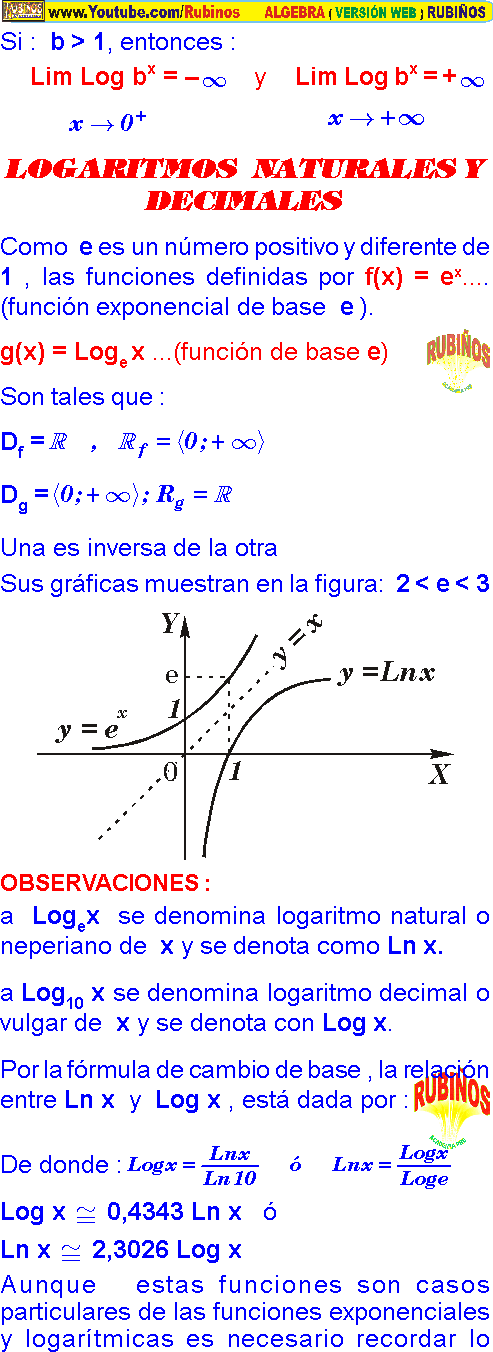
Funciones Exponenciales y Logarıtmicas Los elementos radiactivos tienen la particularidad de que su cantidad disminuye con respecto al tiempo en una forma llamada exponencial porque la ley que lo describe utiliza al número e, llamado número neperiano, La gr´afica de una funci´on exponencial f es creciente o decreciente en todo su dominio y, en consecuencia, f es biyectiva. En particular es inyectiva, esto significa que para n´umeros reales x1 y x2; si ax1 = ax2 entonces x1 = x2. Esta propiedad es de mucha utilidad para resolver ecuaciones exponenciales en ´algebra. En la seccion anterior analizamos que la funcion exponencial dada por f(x) = ax para 0 < a < 1 ´o a > 1 es biyectiva; en consecuencia, f tiene una funci´on inversa f¡1. Esta inversa de la funci´on exponencial con base a se llama funci´on logar´ıtmica con base a y se denota loga. Sus valores se escriben loga(x), que se lee “el logar´ıtmo de x con base a”. Una definici´on formal es la siguiente: Definici´on 1 Sea a un n´umero real positivo diferente de 1. El logar´ıtmo de x con base a se define como Ya que la funci´on logar´ıtmica con base a es la inversa de la funci´on exponencial con base a, la gr´afica de y = loga(x) se obtiene reflejando la gr´afica de y = ax con la linea y = x. La figura siguiente muestra esta gr´afica para a > 1: 6