GEOMETRÍA PREGUNTAS RESUELTAS PUCP DE EXAMEN DE ADMISIÓN A LA UNIVERSIDAD CATÓLICA
PREGUNTA 1 :
En un triángulo acutángulo ABC se trazan las alturas AN y CM, tal que AM=2 u, MB=3 u y BC=6 u. Calcula BN.
A) 2,25 u
B) 2,5 u
C) 2,75 u
D) 3,5 u
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 2 :
Sobre una recta se tienen 4 ángulos consecutivos que se encuentran en una progresión aritmética. Si el primer ángulo es el doble del último, calcula la diferencia de los ángulos intermedios.
A) 5º
B) 8º
C) 10º
D) 12º
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3 :
En una pirámide cuadrangular regular el apotema de la base es 6 cm y el apotema del sólido es 10 cm. Calcula el volumen de la pirámide.
A) 250 cm³
B) 384 cm³
C) 275√3 cm³
D) 420 cm³
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 4 :
A) 52º30’
B) 56º15’
C) 58º20’
D) 60º21’
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 5 :
En un triángulo ABC, AB= 25, m∠A= 106º y m∠B= 37º. Calcula el área del triángulo ABC.
A) 150 m²
B) 200 m²
C) 250 m²
D) 300 m²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 6 :
En un triángulo rectángulo, el producto de catetos es 120 y la suma de dichos catetos es 23. Calcula la longitud de la hipotenusa.
A) 15
B) 13
C) 12
D) 17
RESOLUCIÓN :
Rpta. : "D"
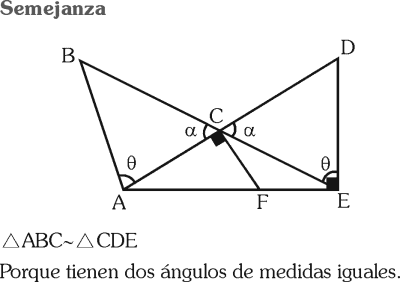
PREGUNTA 7 :
En un triángulo rectángulo ABC, recto en B, la mediatriz del segmento AC y la bisectriz del ángulo A se interceptan en un punto del lado BC. Calcula el menor ángulo del triángulo.
A) 10º
B) 20º
C) 30º
D) 40º
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
En los cuadrados mostrados, AB= 6 y EC= 5. Calcula DP.
A) √13
B) √17
C) √14
D) √19
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 9 :
En un rectángulo ABCD se hace coincidir el vértice B con D, tal como se muestra en la figura. Si BC= 20 cm y AB= 10 cm, calcula PC.
A) 6,5
B) 7
C) 7,5
D) 8
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
A) 20
B) 30
C) 40
D) 50
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 11 :
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 :
Si la longitud de una circunferencia es igual al perímetro de un cuadrado, el área que limita la región de la circunferencia es A y el área del cuadrado es B. Calcula B/A
A) 4/𝛑
B) 2/𝛑
C) 𝛑/2
D) 𝛑/4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 13 :
Se tiene una propiedad en litigio por 3 hermanos. Llega un perito y soluciona el problema dividiendo la propiedad en 3 regiones triangulares. Supongamos que la propiedad es un triángulo ABC en el cual se traza la ceviana AR (R en BC), se toma un punto S en AR. Si AR=3(AS) y RC=4(BR), calcula la mayor área de los triángulos divididos. El área total de la propiedad es de 60 hectáreas.
A) 24 hectáreas
B) 12 hectáreas
C) 48 hectáreas
D) 36 hectáreas
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 14 :
El desarrollo lateral de un prisma cuadrangular regular es un cuadrado de lado 18 m. Calcula el volumen del prisma.
A) 360,5 m³
B) 362,5 m³
C) 364,5 m³
D) 371,6 m³
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 15 :
Si con un galón de pintura se pintan 30 m². ¿Cuántos galones se necesitarán para pintar las paredes de una habitación que tiene por dimensiones 20 m, 10 m y 3 m respectivamente, si la habitación tiene una puerta de 1,5 m×2 m, una ventana de 8,5 m×2 m y dos ventanas de 2,5 m×2 m?
A) 1
B) 3
C) 4
D) 5
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 16 :
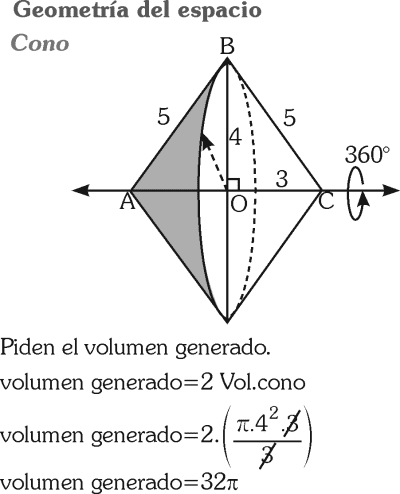
Se tiene un triángulo rectángulo de catetos 3 m y 4 m. ¿Cuál es el volumen del sólido generado al rotar sobre su hipotenusa una vuelta completa?
A) 48𝛑/5
B) 24𝛑/5
C) 12𝛑/5
D) 36𝛑/5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 17 :
Se tiene una semicircunferencia de centro O, calcula “x” (T; P: puntos de tangencia).
A) 37°
B) 53°
C) 30°
D) 45°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 18 :
Se gira una región rectangular de área 10 u², en torno a uno de sus lados, cuya longitud es 2 u. Calcula el área de la superficie lateral del cilindro y su volumen.
A) 20π u² y 20π u³
B) 20π u² y 24π u³
C) 24π u² y 20π u³
D) 18π u² y 20π u³
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 19 :
Se tiene un triángulo ABC, m∠A=60°, AB=2 cm y AC=5 cm. Calcula BC.
A) √21
B) √17
C) √19
D) 2√5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 20 :
En el gráfico, calcula “x”.
A) 82°
B) 76°
C) 75°
D) 81°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 21 :
Se tiene una semicircunferencia de diámetro AB y de radio 4. Calcula x+y.
A) 3√2 ( √3 + √5 )
B) 2√3 ( √2 + √5 )
C) 2√2 ( √3 + √5 )
D) 2(√3 + √5 )
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 22 :
Se tiene un cuadrado ABCD, se construye externamente un triángulo rectángulo AEB. Si EB=14 y AE=10, calcula ED.
A) 26
B) 24
C) 25
D) 21
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 23 :
En una recta se tienen los puntos consecutivos A, B y C. Se construye el triángulo equilátero BEC, si AC=22√3 . Calcula AE
A) 22
B) 33
C) 42
D) 20
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 24 :
De la figura mostrada, MN//BC, AB=4 y BC=6.
Calcula BM.
A) 1,2
B) 1,8
C) 2,4
D) 3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 25 :
Se tiene un paralelogramo ABCD, de modo que AB=12 y BC=5; se traza la bisectriz interior AE (E en DC). Si el área de la región paralelográmica es 48 u², calcula el área de la región AECB.
A) 44 u²
B) 28 u²
C) 36 u²
D) 38 u²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 26 :
En un triángulo rectángulo ABC recto en B. Si M es punto medio de AB y N∈BC, tal que MN es paralela a AC; AN=22 y MC=19. Calcula AC.
A) 21
B) 24
C) 25
D) 26
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 27 :
Se tiene un triángulo equilátero ABC de lado 12, MN//AC . Si AM=10.
Calcula el área de la región del triángulo ABN.
A) 3√3
B) 6√3
C) 4√3
D) 5√3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 28 :
En un cuadrado ABCD, si la intersección entre AC y BM es N; AM=MD y la distancia de N a AM es 20 u.
Calcula el área de la región cuadrada ABCD.
A) 1800 m²
B) 3600 m²
C) 4800 m²
D) 2700 m²
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 29 :
Se tiene un sector circular cuyo ángulo central es 2𝛑/5 rad . Calcula la relación de áreas de dicho sector y el círculo al cual pertenece.
A) 2/5
B) 1/4
C) 1/6
D) 1/5
RESOLUCIÓN :
Rpta. : "A"
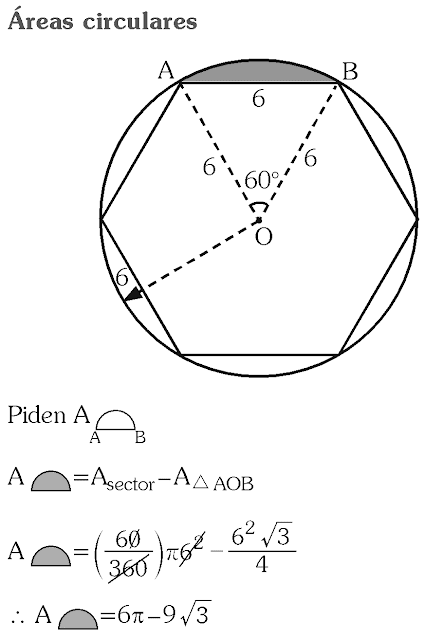
PREGUNTA 30 :
En un hexágono regular inscrito en una circunferencia de radio 6 u, calcula el área de uno de los segmentos circulares determinados por un lado del hexágono regular y la circunferencia.
A) 7π – 6√3
B) 6π – 9√3
C) 8π – 9√3
D) 9π – 6√3
RESOLUCIÓN :
Rpta. : "B"
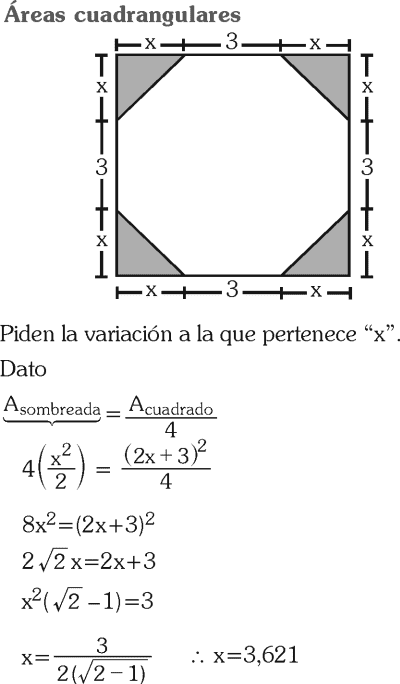
PREGUNTA 31 :
En el gráfico, la suma de las áreas de las regiones sombreadas isósceles es igual a la cuarta parte del área de la región cuadrada ABCD; encuentra a qué intervalo pertenece “x”.
A) 0,5 < x < 1
B) 1 < x < 2,5
C) 2,5 < x < 3,1
D) 3,1 < x < 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 32 :
En la pirámide P–ABC, de altura PA , M es punto medio de PC y AM=BC. Si m∠ABC=90°, calcula el orden de las medidas de los ángulos CPB , PCB y PBC.
A) 45°, 45°, 90°
B) 30°, 75°, 75°
C) 30°, 60°, 90°
D) 60°, 60°, 60°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 33 :
En una semicircunferencia de diámetro AB=12 cm se inscribe el triángulo ACB, por el centro de la semicircunferencia se traza una paralela de AC interceptando a BC en Q y en P a la tangente trazada a la circunferencia en B. Si BC=8, calcula PB.
A) 2√2
B) 3√2
C) 5√2
D) 10
RESOLUCIÓN :
Rpta. : "B"
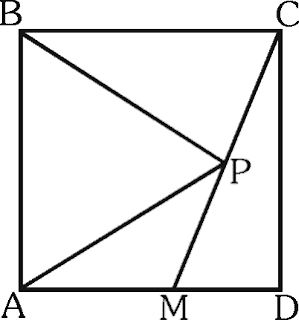
PREGUNTA 34 :
Sea ABCD un cuadrado y el triángulo ABP es equilátero, calcula m∠CMD.
A) 15°
B) 45°
C) 60°
D) 75°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 35 :
Del gráfico mostrado, el triángulo AMD es equilátero y CD=8 u. Sean A₁ y A₂ las regiones sombreadas, calcula A₁×A₂.
A) 64 u²
B) 108/3 u²
C) 128/3 u²
D) 149/3 u²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 36 :
Un cono circular recto invertido se llena de agua hasta la mitad su altura, de 10 cm y radio en la base 4 cm. Si se introduce un cilindro de altura 1 cm y radio en su base 2 cm, calcula la altura del desnivel del agua sufrido en el cono invertido.
a) 3∛133 – 4,5
b) 3∛133 – 5
c) 3∛133 – 4
d) 3∛133 – 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 37 :
Si el volumen de un cilindro recto es el doble del volumen de un cono recto, tal que los radios de sus respectivas bases tienen igual medida; calcula la relación entre las alturas del cilindro y cono, respectivamente.
a) 1/4
b) 2/3
c) 3/4
d) 1
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 38 :
Se tiene un triángulo rectángulo isósceles y un cuadrado, cuyas regiones son equivalentes. Calcule la relación de la hipotenusa y la diagonal del cuadrado.
A) 1
B) √2
C) 2√2
D) 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 39 :
En un trapecio se cumple que el segmento que une los puntos medios de las diagonales y la mediana están en relación de 3 a 5. Calcule la relación de sus bases.
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 40 :
Del gráfico mostrado, calcule “x” si AF=AC y BD=BC.
A) 20°
B) 24°
C) 26°
D) 28°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 41 :
Del gráfico mostrado, calcule CD si AC=24 μ, BC=8 μ y O es centro.
A) √2
B) 2√2
C) 3√2
D) 4√2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 42 :
En el gráfico mostrado, AM=MC, BL=LM, AΔBLE=8μ² , 2(EC)=3(BE) ; calcule AΔABC.
A) 80
B) 70
C) 65
D) 64
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 43 :
En el gráfico, AH=3, AP=2, AL=AM+2; calcule AM.
A) 2,5
B) 3
C) 4
D) 4,5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 44 :
Se tiene un cilindro de radio 6 y generatriz 30 que contiene cierto líquido. Se desea vaciar el líquido en vasos de forma de tronco de cono de radio menor 2, radio mayor 4 y altura 8, con la condición de que solo los vasos se llenan hasta sus tres cuartas partes. Calcula la cantidad de vasos empleados aproximadamente.
A) 18
B) 19
C) 20
D) 21
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 45 :
Una cometa es soltada tal que la cuerda que sostiene a la cometa se estira 50 m. Si el ángulo de inclinación que forma la cuerda con la horizontal es 37°, calcule a qué altura se encuentra la cometa.
A) 10
B) 20
C) 30
D) 40
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 46 :
Se tiene una esfera inscrita en un cilindro de revolución. Si el área de la superficie esférica es 100𝛑 μ², calcule el volumen del cilindro.
A) 200𝛑 μ³
B) 250𝛑 μ³
C) 300𝛑 μ³
D) 450𝛑 μ³
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 47 :
Del gráfico mostrado, calcule MC − AM si AB=18 μ, BC=27 μ y AC=35 μ.
A) 2 μ
B) 5 μ
C) 6 μ
D) 7 μ
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 48 :
Calcule la medida del ángulo determinado por dos diagonales adyacentes de las caras de un hexaedro regular.
A) 90°
B) 45°
C) 60°
D) 120°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 49 :
En una circunferencia de radio 2 se inscribe un rectángulo cuyo lado menor es 2. Calcule el área de la región determinada entre dos lados consecutivos del rectángulo y la circunferencia.
A) 𝛑 − √3
B) 2(𝛑 − √3)
C) √3 (𝛑 − √3)
D) 4√3 (𝛑 − √3)
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 50 :
Del gráfico mostrado, si AB=5 , CD=2 y BC=7, calcule FC.
A) 2,5
B) 1,5
C) 2
D) 3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 51 :
En un triángulo isósceles de lados 15 cm y 32 cm, calcule su perímetro.
A) 50 cm
B) 62 cm
C) 79 cm
D) 80 cm
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 52 :
Del gráfico mostrado, calcule el volumen del sólido generado al rotar la región triangular ABC alrededor del segmento AC.
A) 30𝛑
B) 32𝛑
C) 36𝛑
D) 38𝛑
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 53 :
Se tiene hexágono regular cuyo perímetro es 12√3 . Calcule el área de la región triangular cuyos vértices son los puntos medios de los lados no consecutivos.
A) 25√3 /4
B) 27√3/4
C) 28√3
D) 39√3 /4
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 54 :
Del gráfico mostrado, calcule el área de la región sombreada si AC=25 , AB=24 , BC=7, M es punto medio del segmento AB y MD=13.
A) 16 u²
B) 15/7 u²
C) 48/7 u²
D) 20 u²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 55 :
Del gráfico, BG=15, GL=18, EF=6 y AD=4(DF); calcule AB ( ▱ABCD: paralelogramo). 
A) 9
B) 10
C) 11
D) 12
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 56 :
Se tiene un triángulo ABC y los ángulos son proporcionales a los números 5 ; 4 y 3, respectivamente. Calcula la medida del ángulo formado por la altura y la bisectriz relativa al lado intermedio.
A) 10°
B) 15°
C) 20°
D) 25°
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 57 :
A) 15°
B) 20°
C) 30°
D) 35°
RESOLUCIÓN :
Rpta. : "B"
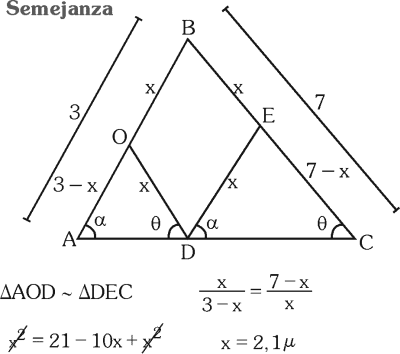
PREGUNTA 58 :
A) 2 μ
B) 2,1 μ
C) 2,5 μ
D) 3 μ
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 59 :
A) 3 μ
B) 4 μ
C) 7 μ
D) 8 μ
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 60 :
En un triángulo isósceles ABC, se trazan las medianas AM y CN perpendiculares. Si AC=1 y AB=BC, calcula el área de la región triangular ABC.
A) 2 μ²
B) 3/2 μ²
C) 3/4 μ²
D) 3/8 μ²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 61 :
En un triángulo rectángulo recto en B, se traza la altura BH (H en AC). Si HC=28 y BH=14, calcula el área de la región triangular ABC.
A) 230 μ²
B) 245 μ²
C) 260 μ²
D) 250 μ²
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 62 :
En un trapecio isósceles ABCD. Si AB=5, BC=4 y AD=10.
Calcule el área del trapecio.
A) 25u²
B) 26u²
C) 27u²
D) 28u²
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 63 :
Se tiene un trapecio ABCD, se traza BD de tal manera que la m∠CBD=35º, m∠BCD=110º y AD=2BC=2CD. Calcule la medida del ángulo BAD.
A) 40º
B) 45º
C) 50º
D) 55º
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 64 :
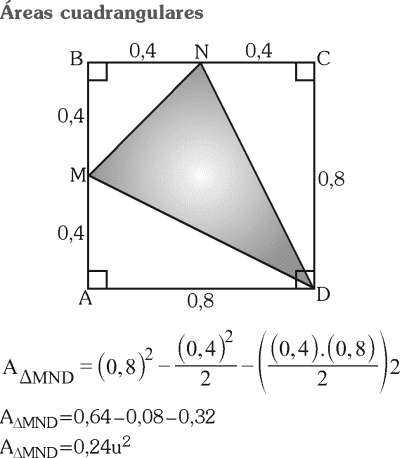
Del gráfico, si M y N son puntos medios de los segmentos AB y BC respectivamente, si AB=BC=0,8.
Calcule el área de la región triangular MND
A) 0,24u²
B) 0,25u²
C) 0,26u²
D) 0,18u²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 65 :
Se tiene un triángulo equilátero de área 3√3u² . Determine el área de la región circular circunscrita a dicho triángulo
A) 2𝛑
B) 3𝛑
C) 6𝛑
D) 4𝛑
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 66 :
Se tiene dos esferas cuya relación de volúmenes es de 1 a 2, si el radio de la menor es ∛16 .
Calcule el volumen de la esfera mayor.
A) 143𝛑/3
B) 196𝛑/3
C) 129𝛑/3
D) 128𝛑/3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 67 :
Se tiene una pirámide regular V-ABCDEF, se ubica los puntos medios M,N y S en las aristas VA, VE y VD, luego se grafica el prisma triangular recto MNS-PQR tal que P, Q y R están en la base de la pirámide. El área de la superficie lateral y la altura del prisma es de 30√3 y 10 respectivamente. Calcule el volumen de la pirámide.
A) 10√3
B) 40
C) 20√3
D) 40√3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 68 :
En un prisma hexagonal regular, la arista lateral es el doble de su arista básica, si su volumen es 24√3 . Calcule el área de su superficie lateral.
A) 56u²
B) 36u²
C) 48u²
D) 64u²
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 69 :
Un trapecio isósceles se encuentra inscrito en una circunferencia. Si la diferencia de los arcos de las bases es 160°, calcular uno de los ángulos agudos.
A) 30°
B) 50°
C) 70°
D) 80°
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 70 :
En un triángulo rectángulo ABC (recto en B) se inscribe el cuadrado PQRS (PS en el segmento AC), si AP=50 y SC=72. Calcula el lado del cuadrado.
A) 40
B) 50
C) 60
D) 70
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 71 :
Una esfera de 100𝛑m² de área está inscrita en un cilindro. Calcular el volumen del cilindro.
A) 200𝛑m³
B) 220𝛑m³
C) 250𝛑m³
D) 260𝛑m³
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 72 :
Cinco ángulos consecutivos en progresión aritmética forman un ángulo llano. Si el mayor es el cuadrado del menor, calcular la medida del menor ángulo.
A) 4
B) 8
C) 6
D) 10
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 73 :
Un ∆ ABC tiene por coordenadas A(–5;1) , B(–5;4) y C(2;4). Calcular el área del triángulo.
A) 10,5 u²
B) 12,5 u²
C) 14,5 u²
D) 16 u²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 74 :
En un triángulo rectángulo ABC se traza la altura BH y la mediana BM, si m∠C= 20°. Calcula m∠HBM.
A) 40°
B) 60°
C) 50°
D) 70°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 75 :
Si ABCD es un rectángulo inscrito en la semicircunferencia de radio igual a 2 cm, calcula el área de la región sombreada. (“θ” está en radianes).
A) 2θ–sen2θ
B) 4θ–5senθ
C) 5θ–2senθ
D) 3θ–4senθ
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 76 :
Colocando cinco cubos verticalmente, se determina un prisma de diagonal 18; calcula el área total del prisma.
A) 216 u²
B) 172 u²
C) 241 u²
D) 264 u²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 77 :
En el cuadrado, ABCD la suma de las áreas de los triángulos rectángulos isósceles sombreados es la cuarta parte del área del cuadrado; calcula “x”.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 78 :
El suplemento de un ángulo más el complemento de otro ángulo es 140°. Calcula el suplemento de la suma de los dos ángulos.
A) 20°
B) 30°
C) 40°
D) 50°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 79 :
En un triángulo rectángulo ABC, recto en B, la altura relativa a la hipotenusa mide √24 y determina dos segmentos proporcionales a 2 y 3. Calcula el cateto BC.
A) 4√2
B) 2√15
C) 7√5
D) 9√3
RESOLUCIÓN :
Rpta. : "B"