TRIGONOMETRÍA PREGUNTAS RESUELTAS PUCP DE EXAMEN DE ADMISIÓN A LA UNIVERSIDAD CATÓLICA
PREGUNTA 1 :
Si: cosx ctgx = 3
determina cscx – senx.
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2 :
Se tienen dos ángulos que sumados son 5𝛑/4 rad y su diferencia es 75°. Determina el suplemento del mayor de los ángulos en radianes.
A) 𝛑/12 rad
B) 𝛑/6 rad
C) 𝛑/4 rad
D) 𝛑/3 rad
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
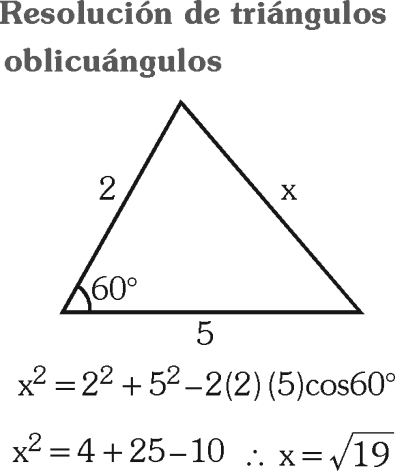
Del gráfico, determina “x”.
A) √11
B) √13
C) √17
D) √19
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
Calcula:
A) 1/11
B) 1/44
C) 19/44
D) 19/11
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 :
Si se cumple
ctgx +tgx + csc2x = 4
Determina :
A) 1/7
B) 7
C) 3
D) 2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
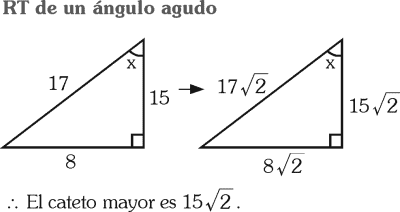
En un triángulo rectángulo, la tangente de uno de sus ángulos agudos es 8/15. Determina su cateto mayor si la hipotenusa es 17√2 .
A) 12√2
B) 10√2
C) 15√2
D) 8√2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7 :
M= cos(θ)cos(2θ)cos(3θ)cos(4θ)csc(5θ)
Halla 64M, si θ= 15°
A) √6
B) 1
C) 8√6
D) 8
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
Si 0 < x < 𝛑/2
calcula:
cos(x+𝛑)+cos(x+𝛑/2)+cos(x – 𝛑)+tg(x+𝛑)cos(x+𝛑)
A) senx – 2cosx
B) 3senx
C) 2senx
D) –2senx – 2cosx
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9 :
Determinar la relación entre el área de un sector circular, cuyo ángulo central es 2𝛑/5 radianes, y el área de un círculo, sabiendo que tienen el mismo radio.
A) 2/5
B) 1/5
C) 3/5
D) 5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 10 :
En el cuadro siguiente, unir mediante flechas.
A) IB, IID, IIIF
B) IC, IID, IIIB
C) ID, IIA, IIIC
D) IB, IIC, IIID
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
Un observador de 1,7 m de estatura visualiza la parte alta de una antena colocada sobre un edificio, con ángulo de elevación de 37º; si se acerca 7 m hacia el edificio, el nuevo ángulo de elevación es 53º. Si la antena mide 1,5 m, determinar la altura del edificio.
A) 12,2 m
B) 13,2 m
C) 14,2 m
D) 15,2 m
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12 :
Determinar la expresión correcta
I) Si x∈ ] 3𝛑/2 ; 2𝛑 [ ⇒ tgx es positiva.
II) Si x∈ ] 𝛑/2 ; 𝛑 [ ⇒ senx es creciente.
III) Si x∈ ] 𝛑 ; 3𝛑/2 [ ⇒ cosx es negativa.
A) Solo III
B) Solo I
C) Solo II
D) I y III
RESOLUCIÓN :
Circunferencia trigonométrica
I) Si x∈ ] 3𝛑/2 ; 2𝛑 [ ⇒ tgx es negativa.
II) Si x∈ ] 𝛑/2 ; 𝛑 [ ⇒ es decreciente.
III) Si x∈ ] 𝛑 ; 3𝛑/2 [ ⇒ cosx es negativa.
Rpta. : "A"
PREGUNTA 13 :
Del gráfico mostrado, hallar tgθ, si tgα= 5/8
A) 5/4
B) 5/2
C) 3/2
D) 5/3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 14 :
Sea la función, y=f(x)=tgx
Se sabe que:
Dom∈ [0;a] ∪ [b;π]
Ran ∈ [–√3 ;√3 ].
Hallar: a+b
A) π/4
B) π/3
C) π
D) 2π
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 15 :
Calcular:
2(a – b)senπ/2 +3(a – b)cosπ – (b – a)cscπ/2
A) a–b
B) 2(a+b)
C) 4(a–b)
D) 0
RESOLUCIÓN :
R.T. de un ángulo de cualquier magnitud
=2(a – b)(1) +3(a – b)(–1) – (b – a)(1)
=2a – 2b – 3a+3b – b+a
=0
Rpta. : "D"
PREGUNTA 16 :
Una persona parte desde A hacia B con rumbo S60º0, luego se dirige hacia C con rumbo S75ºE, hasta ubicarse al sur de A. Si la distancia entre A y C es 10 m; halle aproximadamente la distancia entre B y C.
A) 10 m
B) 20 m
C) 15 m
D) 12 m
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 17 :
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 18 :
Sabiendo que 0 ≤ 2θ ≤ π; además, senθ.cosθ= 1/4
Calcule
E = senθ + cosθ
A) 3/2
B) √(3/2)
C) √3/2
D) √2/2
RESOLUCIÓN :
Identidades de una variable Auxiliares
0 ≤ 2θ ≤ π
⇒ 0 ≤ θ ≤ π/2
E²=(senθ + cosθ)²
⇒ E²= 1 + 2senθ.cosθ
⇒ E²= 1 + 2 × 1/4
→ E²= 3/2 ⇒ E=±√3/2
Como θ∈IC
∴ E =√(3/2)
Rpta. : "B"
PREGUNTA 19 :
Si (2tgα+1)(tgα+2)cos²α=3
Calcule senαcosα.
A) 0,60
B) 0,30
C) 0,25
D) 0,20
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 20 :
En el siguiente gráfico se sabe que x² =a+b√2
Calcule E=a − b.
A) 90
B) 91
C) 92
D) 93
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 21 :
Un niño está volando una cometa. En determinado momento, la cuerda que sujeta la cometa mide 50 m, formando con el suelo un ángulo de 37º. Determine a qué altura se encuentra la cometa.
A) 40 m
B) 50 m
C) 20 m
D) 30 m
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 22 :
Reduzca:
A) 1
B) 0
C) − 1
D) 2
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 23 :
Siendo la identidad sen(x+60º) − cos(x+30º)=asenx+bcosx
Determine: a − b
A) 0
B) 1
C) 2
D) − 1
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 24 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 25 :
A) 1
B) – 1
C) 2
D) – 2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 26 :
Del gráfico, calcula tgθ si cos37°=4/5
A) 1/3
B) 2/3
C) 1
D) 3/4
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 27 :
Del gráfico, calcula cosθ.
A) √3
B) 2√7/7
C) √7
D) 7√5 /5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 28 :
Calcule la suma de las dos primeras soluciones positivas de la ecuación.
2Sen2x+2(Senx+Cosx)=– 1
A) 𝛑/6
B) 𝛑/3
C) 5𝛑/6
D) 11𝛑/6
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 29 :
Calcule el número de soluciones en el intervalo: [0 ; 2𝛑] de la siguiente ecuación:
Sen2x=Senx
A) 2
B) 3
C) 4
D) 5
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 30 :
A) 𝛑/6
B) 𝛑/3
C) 𝛑/4
D) 𝛑/12
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 31 :
Del gráfico, determine el Senx
A)√6/6
B)√6/5
C)√6/4
D)√6/3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 32 :
A) 1/3
B) 1/4
C) 1/5
D) 1/2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 33 :
En un triángulo dos de sus lados miden 3cm y 4cm y el ángulo comprendido entre ellos mide θ. si: Cosθ=–11/24 , calcular el perímetro del triángulo.
A) 9
B) 11
C) 13
D) 15
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 34 :
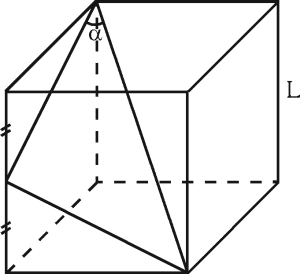
Del cubo mostrado, calcule :
(senα + cosα)÷(tanα + cotα ) ; el lado del cubo es L
A) √6
B) √30/5 [ √3+√2]
C) √6/5 [ √3+√2]
D) √30/25 [ √3+√2]
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 35 :
En un triángulo ABC, de lados 3 y 4 unidades, el coseno del ángulo que forman dichos lados es – 11/24. Calcule el perímetro de dicho triángulo.
A) 10
B) 13
C) 15
D) 17
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 36 :
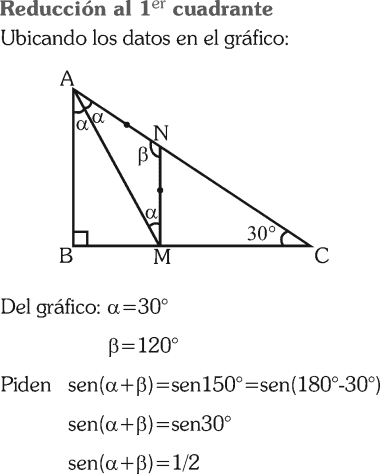
En el gráfico, AM es bisectriz del ángulo BAC; el ∠ACB=30°. Además α=∠NAM y β=∠MNA, siendo AN=NM; calcule sen(α+β)
A) 1/2
B) 3 /2
C) 2 /2
D) 3/5
RESOLUCIÓN :
Rpta. : "A"