3RO 4TO ACTIVIDAD 4 EXPERIENCIA 6 MATEMATICA APRENDO EN CASA TERCERO CUARTO DE SECUNDARIA TAREA WEB RETO TV RADIO APRENDIZAJE PDF

ACTIVIDAD 4 
EXPERIENCIA DE APRENDIZAJE INTEGRADA 6 | 3°–4° grado 
PLANTEAMOS CONCLUSIONES SOBRE LA UTILIDAD DE LAS FUNCIONES CUADRÁTICAS AL DETERMINAR EL ESPACIO PARA REALIZAR ACTIVIDADES FÍSICAS 
¡Hola! 
En la actividad anterior, determinamos el espacio para realizar actividad física, mediante el modelado de la función cuadrática. 
En esta actividad, plantearemos conclusiones sobre la utilidad de estas funciones y su gráfica, para encontrar el espacio que nos permita realizar actividades físicas y considerarlas en nuestro plan para mejorar la salud en familia. 
CONTINUAMOS CON LA SITUACIÓN DE MARÍA 
María ha obtenido las dimensiones del espacio rectangular que delimitó con la cuerda de 20 metros que tenía. 
Hallo el área máxima de este espacio rectangular y encontró que la expresión algebraica que le permite calcular el área máxima del rectángulo es la siguiente: ƒ(x) = − 2x2 + 20x 
A partir de esta información que tiene, se hace las siguientes preguntas: 
¿Cómo interpretamos la información de la gráfica de la función cuadrática en esta situación? 
¿Qué afirmaciones, conclusiones o recomendaciones podríamos plantear sobre la utilidad de funciones cuadrática al calcular espacios para realizar actividades físicas u otros? 
Antes de iniciar la actividad, recordemos los saberes previos sobre las funciones cuadráticas. Para ello, leemos el texto “Función cuadrática” disponible en la sección “Recursos para mi aprendizaje”. 
Con la información, respondemos las preguntas referidas a la situación: 
1. ¿De qué forma se presenta la función cuadrática? 
2. ¿Qué forma tiene la gráfica de la función cuadrática? 
3. Recordemos que la expresión matemática que permite resolver la situación es: ƒ(x) = − 2x2 + 20x 
¿Cómo empleamos esta expresión para graficar la función cuadrática? 
¿Crees que sea la única forma de realizar este gráfico?, ¿por qué? 
Realiza una descripción de esta propuesta considerando tus saberes previos. 
Anota en tu cuaderno. 
TOMEMOS EN CUENTA QUE... 
Una forma de graficar de manera directa, y considerando los coeficientes de una función cuadrática, es realizando el siguiente proceso: 
• Primero. Encontramos el vértice de la parábola. 
• Segundo. Identificamos hacia dónde abre la parábola. 
• Tercero. Determinamos los cortes con los ejes X, Y. 
• Cuarto. Graficamos en el plano cartesiano, identificando las coordenadas halladas. 
PROCESOS RECOMENDADOS PARA GRAFICAR UNA FUNCIÓN CUADRÁTICA 
Para graficar la función cuadrática que representa la situación de María, leemos el texto “Gráfica de la función cuadrática”, disponible en la sección “Recursos para mi aprendizaje”. 
TOMEMOS EN CUENTA QUE... 
Una función cuadrática tiene la forma ƒ(x) = ax2 + bx + c, donde los coeficientes a, b y c son números reales y a ≠ 0. Su gráfica es una parábola con vértice V(h; k). 
Las coordenadas del vértice V se determina mediante las expresiones: x = h =– b y k −b + 4ac vértice 2a vértice = = 4a 
REPRESENTAMOS NUESTRA GRÁFICA 
Aplica los procesos que identificaste en el paso anterior y grafica la función cuadrática ƒ(x) = −2x2 + 20x. Para ello, realiza lo siguiente: 
1. Determina las coordenadas del vértice de la parábola, identifica hacia dónde se abre la parábola y encuentra los cortes con los ejes X e Y. 
2. Ahora, con los datos anteriores, en una hoja o cuaderno cuadriculado elabora un plano cartesiano, ubica las coordenadas halladas y realiza el trazo de la parábola que representa a la función. 
3. Compara tu representación gráfica elaborada en tu cuaderno con la representación gráfica que obtuviste en GeoGebra en la actividad anterior. Luego, respondemos las interrogantes: 
• ¿Qué características comunes identificas en ambas gráficas de la función cuadrática? 
• ¿Cómo interpretamos el valor del vértice de la parábola para responder la pregunta de la situación?
 3. ¿Qué afirmaciones, conclusiones o recomendaciones podríamos plantear sobre la utilidad de funciones cuadrática al calcular espacios para realizar actividades físicas u otros? 
Nos ayudamos con las siguientes preguntas: 
• ¿Cómo nos ayudó la función cuadrática a resolver la situación? 
• ¿En qué situaciones de la vida diaria podemos utilizar las funciones cuadráticas? 
• ¿Qué tipos de ejercicios físicos podríamos realizar en el espacio delimitado por la cuerda? Registra en tu cuaderno de trabajo o portafolio. 
REFLEXIONAMOS SOBRE LOS RESULTADOS OBTENIDOS 
1. ¿En qué situaciones de la vida diaria podemos utilizar las funciones cuadráticas? 
2. ¿Qué tipos de ejercicios físicos podríamos realizar en el espacio delimitado por la cuerda? 
3. ¿Qué dificultades tuvimos al momento de resolver la situación presentada? ¿Cómo superamos estas dificultades? 
4. Para culminar, resolvemos las actividades del Cuaderno de trabajo de Matemática del grado que nos corresponde. Resolvamos problemas 3 (páginas 32 y 33). 
REFLEXIONAMOS EN FAMILIA 
Dialogamos en familia sobre la importancia de realizar actividad física para el beneficio de la salud y el compromiso de ubicar el espacio necesario y apropiado. 
¿Qué sugerencia podemos dar a las personas para que se animen a realizar actividades físicas? 
EVALUAMOS NUESTROS AVANCES 
Ahora, nos autoevaluamos para reconocer nuestros avances y lo que requerimos mejorar. Coloca una “X” de acuerdo con lo que consideres. 
Luego, escribe las acciones que tomarás en cuenta para mejorar tu aprendizaje. 
Competencia: 
Resuelve problemas de regularidad, equivalencia y cambio. 
Criterios de evaluación 
Lo logré 
Estoy en proceso de lograrlo 
¿Qué puedo hacer para mejorar mis aprendizajes? 
Establecí relaciones entre datos, valores desconocidos y variación entre magnitudes y las transformé a funciones cuadráticas. 
Evalué si la expresión algebraica que planteé representa las condiciones del problema como los datos, términos desconocidos o variación entre dos magnitudes. 
Expresé con representaciones gráficas, tabulares y con lenguaje algebraico mi comprensión sobre comportamiento gráfico de una función cuadrática. 
Expresé con representaciones gráficas los valores máximos, mínimos e interceptos, su eje de simetría, vértice y orientación, para interpretar su solución en relación a la situación. 
Seleccioné y combiné estrategias, métodos, recursos y procedimientos más convenientes para representar funciones cuadráticas, según las condiciones del problema. 
Planteé afirmaciones sobre las relaciones de cambio que se observa entre las variables de la función cuadrática. 
Justifiqué o descarté la validez de mis afirmaciones mediante propiedades o razonamiento inductivo y deductivo. 
VAMOS A LA SIGUIENTE ACTIVIDAD 
¡Felicitaciones! 
Hemos logrado plantear conclusiones sobre la utilidad de las funciones cuadráticas al determinar el espacio para realizar actividades físicas. 
En la siguiente actividad, explicaremos cómo el organismo permite regular la temperatura. ¡Estamos listos, vamos a seguir aprendiendo! 
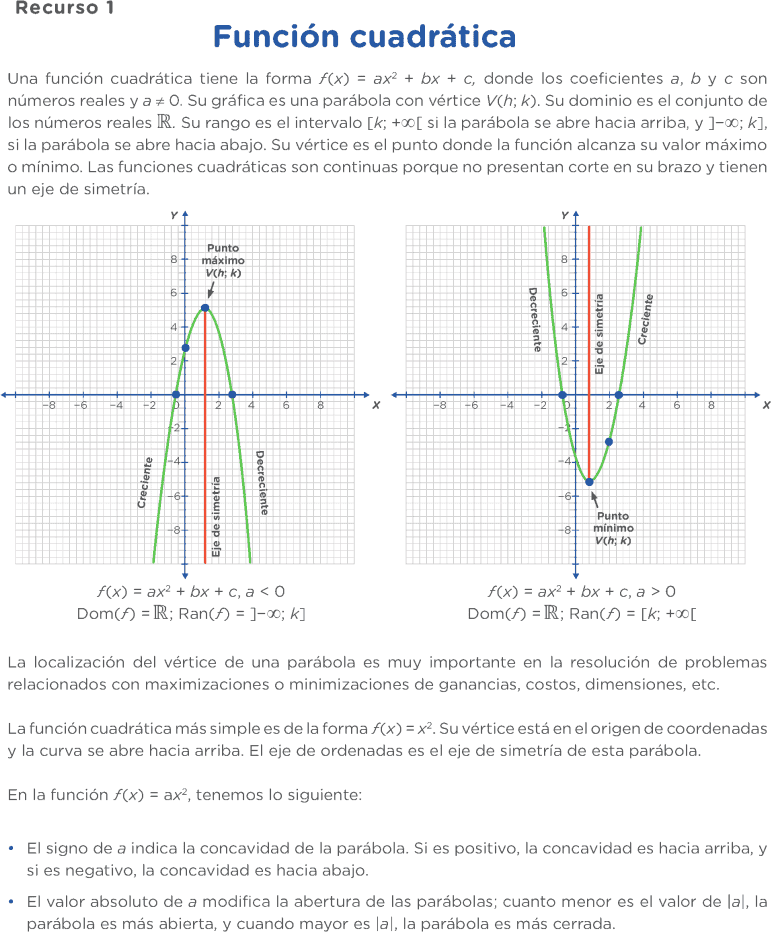
FUNCIÓN CUADRÁTICA 
Una función cuadrática tiene la forma ƒ(x) = ax2 + bx + c, donde los coeficientes a, b y c son números reales y a ≠ 0. 
Su gráfica es una parábola con vértice V(h; k). Su dominio es el conjunto de los números reales . 
Su rango es el intervalo [k; +∞[ si la parábola se abre hacia arriba, y ]−∞; k], si la parábola se abre hacia abajo. 
Su vértice es el punto donde la función alcanza su valor máximo o mínimo.
Las funciones cuadráticas son continuas porque no presentan corte en su brazo y tienen un eje de simetría.

Preguntas resueltas de secundaria y pre universidad